イメージでわかる数学と解析力学：社会人になってから学ぶ数学と物理学（中級編）

🌟 イメージでわかる数学と解析力学：社会人になってから学ぶ数学と物理学（中級編） 🌟

コース概要

AIの機械学習や量子コンピュータなど、今の日常生活に直接関わっている先端テクノロジーは、基盤として必要経度として「数学」を頼りにしています。学生の時代に数学が苦手で避けていただけた方も多いですね。しかし、成長後、その知識への興味が湧いてきたことは稀です。市販の教科書はよく抽象的で理解がつかず、独学を始めるにも手足をつけやすい状況です。

このコースでは、「解析力学（かいせきりきがく）」を通じて、微分、偏微分、三角関数、ベクトル（線形代数）などの数学の基礎を実際に使う方法を学びます。物理学は抽象的な数学を具体的な現象（力学的運動、波動の波形など）と結びつけることができるため、こちらが数学を「イメージ化」する最善の方法です。

本コースの特長

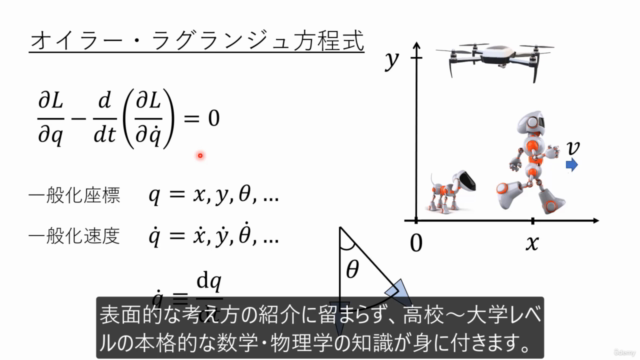
• 豊富なイラストとアニメーション 🎨✨ 市販の参考書にはない、豊富な視覚的マテリアルを通じて、数学の概念が頭の中でどんどん膨らみます。実際の物理現象や数式の適用例をイメージしやすいようにサポートします。

• 具体例と解き方 📚🔍 本コースでは、数式の厳密な定義や証明を省略し、真似切り取ることで自分自身が問題を解く方法を身につけます。多様な例を通じて、実際に数学をどのように使うかがわかるようにサポートします。

• 納得感と実践感 🤝💡 このコースでは、数式の理解度よりも「なぜそのように使えるのか」への納得感や、「これをどんな状況で使い分ければいいのか」といった実践的な知識を身につけていきます。数学は単なる形式の集合ではなく、現実世界の問題解決に役立つツールであることを実感していきます。

コース内容（主要なトピック）

• 微分競技部 微分の基本から応用へ、徐調和式や微分方程式について学びます。具体的な例を通じて、微分がどのように役立ちるのかを理解します。

• 偏微分競技部 多変数関数の微分と偏微分の概念を学び、物理的な現象（例：温度分布の求め方）での応用を紹介します。

• 三角関数・複素数 三角関数の性質や周期性、複素数の基本から応用へと捉えます。具体的な物理現象（例：電気回路のフィールドの適用）での使い方を学びます。

• ベクトル・線形代数 ベクトルの基本からベクトル間の線形関係、行列とその応用（例：電気回路のキャプレーン分析）を学びます。

課外リソースとサポート

• 定期的なQ&Aセッション 教材の内容で疑問や困っている部分があれば、定期的に行われるQ&Aセッションで解決します。

• コミュニティへの参加 他の学習者と情報交換を行い、互いに刺激させ合います。

このコースを通じて、数学や物理を「イメージ化」し、実際の問題解決に活かす能力を身につけることができます。現在この機会を逃すならば！